Skip to contents

Confidence Interval Selection

Source: vignettes/Wald_and_Log_Bound.Rmd
Wald_and_Log_Bound.Rmd

Available Methods

Colossus supports two methods of calculating a confidence interval for model parameters for Cox proportional hazards models. The Wald method and a likelihood-based bound method. This vignette will be focused on the differences and what issues may arise.

Wald Method

When Colossus finishes a Cox regression, it returns both parameter estimates and standard errors. The simplest form of confidence interval is assuming a normal distribution with the parameter mean and deviation. The standard errors are calculated from the covariance matrix, which is calculated as the negative inverse of the information matrix (II) which is equal to the second derivative of Log-Likelihood.

I≈∂2LL∂β→2 \begin{aligned} I \approx \frac{\partial^2 LL}{\partial \vec{\beta}^2} \end{aligned}

For every row (ii) if there is an event (δi=1\delta_i=1) the second derivative is a function of the relative risk and derivatives at the event row (A,BA, B) and the sum of relative risks and derivatives for every row at risk (C,D,EC, D, E) based on the rows in each risk group (l∈Ril \in R_i).

∂2LL∂β→j∂β→k=∑i=0N(δi((Ai,j,k−Bi,j*Bi,k)−(Ci,j,k−Di,j*Di,k)))Ai,j,k=∂2ri∂β→j∂β→kri,Bi,j=∂ri∂β→jriCi,j,k=∑l∈Ri∂2rl∂β→j∂β→kEi,Di,j=∑l∈Ri∂rl∂β→jEi,Ei=∑l∈Rirl \begin{aligned} \frac{\partial^2 LL}{\partial \vec{\beta}_j \partial \vec{\beta}_k} =& \sum_{i=0}^N \left( \delta_i \left( (A_{i,j,k} - B_{i,j}*B_{i,k} ) - (C_{i,j,k} - D_{i,j}*D_{i,k} ) \right)\right)\\ A_{i,j,k} =& \frac{\frac{\partial^2 r_i}{\partial \vec{\beta}_j \partial \vec{\beta}_k}}{r_i}, B_{i,j} = \frac{\frac{\partial r_i}{\partial \vec{\beta}_j}}{r_i}\\ C_{i,j,k} =& \frac{\sum_{l \in R_i} \frac{\partial^2 r_l}{\partial \vec{\beta}_j \partial \vec{\beta}_k}}{E_i}, D_{i,j} = \frac{\sum_{l \in R_i} \frac{\partial r_l}{\partial \vec{\beta}_j}}{E_i}, E_{i} = \sum_{l \in R_i} r_l \end{aligned}

This gives a symmetric parameter confidence interval which is often accurate for single term log-linear models. However this approximation is often inaccurate for models with linear effects, particularly if the confidence interval includes negative values. Because the Wald method approximates the likelihood confidence interval, there is no guarantee that the model is defined over the interval.

Likelihood-Based Bound

The more exact solution is to directly solve for the boundary. The basic premise is that the model can be optimized with a parameter (β\beta) fixed. Each value of β\beta has a corresponding maximum log-likelihood. The confidence interval is the range of values of β\beta such that the maximum log-likelihood is above a threshold, taken from the asymptotic χ2\chi^2 distribution of the generalized likelihood ratio test. Colossus uses the Venzon-Moolgavkar algorithm to iteratively solve for the interval endpoints.

There is one main issues that can arise from this method. The algorithm uses a Newton-Raphson algorithm, which may solve for local solutions instead of the global solution. Similar to the general Colossus regressions, limitations can be placed on step size to limit these effects. However, there is no analogue to selecting multiple starting locations. This is the basis for ongoing work to code in an alternative that can more directly solve for the true optimum.

This method directly solves for the confidence interval, which for linear cases may be non-symmetric or even not have upper or lower bounds. Linear models may be defined only above a parameter threshold. If the optimum value at that parameter threshold is above the χ2\chi^2 threshold value, then the interval would not have a lower bound.

Example and Comparison

For the sake of comparison, we will consider an analysis of the capacitor data available in the survival package. Consider the two regressions, one fully exponential and one with a linear effect. Both regressions converge with nearly identical scores.

data(reliability, package = "survival")

df <- capacitor
df$voltage <- (df$voltage - 200) / 150
df$temperature <- (df$temperature - 170) / 10
df$time <- (df$time - 216) / (1105 - 216)

t0 <- "%trunc%"
t1 <- "time"
event <- "status"

names <- c("temperature", "voltage")
tform <- c("loglin", "loglin")
control <- list("Ncores" = 1, "maxiter" = 100, "verbose" = 0)

a_n <- c(0.01, 0.01)
term_n <- c(0, 0)
keep_constant <- c(0, 0)
modelform <- "M"
fir <- 0

e1 <- RunCoxRegression(
  df, t0, t1, event, names, term_n, tform, keep_constant,
  a_n, modelform, fir, 0, control
)
Interpret_Output(e1, 5)
#> |-------------------------------------------------------------------|
#> Final Results
#>      Covariate Subterm Term Number Central Estimate Standard Deviation
#>         <char>  <char>       <int>            <num>              <num>
#> 1: temperature  loglin           0        0.7599511          0.3964440
#> 2:     voltage  loglin           0        1.9884051          0.6063097
#> 
#> Cox Model Used
#> -2*Log-Likelihood: 210.77792,  AIC: 214.77792
#> Iterations run: 9
#> maximum step size: 1.00000e+00, maximum first derivative: 1.30641e-05
#> Analysis converged
#> Run finished in 0.0667 seconds
#> |-------------------------------------------------------------------|

names <- c("temperature", "voltage")
tform <- c("plin", "loglin")
a_n <- c(0.01, 0.01)

e2 <- RunCoxRegression(
  df, t0, t1, event, names, term_n, tform, keep_constant,
  a_n, modelform, fir, 0, control
)
Interpret_Output(e2, 5)
#> |-------------------------------------------------------------------|
#> Final Results
#>      Covariate Subterm Term Number Central Estimate Standard Deviation
#>         <char>  <char>       <int>            <num>              <num>
#> 1: temperature    plin           0         1.138152          0.8476528
#> 2:     voltage  loglin           0         1.988403          0.6063095
#> 
#> Cox Model Used
#> -2*Log-Likelihood: 210.77792,  AIC: 214.77792
#> Iterations run: 9
#> maximum step size: 1.00000e+00, maximum first derivative: 2.89872e-05
#> Analysis converged
#> Run finished in 0.05823 seconds
#> |-------------------------------------------------------------------|

Next suppose we were interested in the confidence intervals. Suppose we want 95% confidence intervals for both the Wald and likelihood-based boundaries and for both parameters in each model. Let us start with the fully exponential model. The Wald boundary is estimated using the central estimates and standard deviations. The Likelihood boundary is solved using the “log_bound” option under the model control list. The parameter number needs to be provided (indexed starting at zero) and an alpha level needs to be provided. Overall the likelihood boundary were all solved with scores within a narrow margin of the threshold. However the boundaries are not exactly the same. The boundaries for temperature are (-0.017, 1.537) and (-0.001, 1.560), and the boundaries for voltage are (0.800, 3.177) and (0.841, 3.242). The two boundaries are off on the scale of less than 0.1.

names <- c("temperature", "voltage")
tform <- c("loglin", "loglin")
ci_1 <- c(
  e1$beta_0[1] - 1.96 * e1$Standard_Deviation[1],
  e1$beta_0[1] + 1.96 * e1$Standard_Deviation[1]
)
ci_2 <- c(
  e1$beta_0[2] - 1.96 * e1$Standard_Deviation[2],
  e1$beta_0[2] + 1.96 * e1$Standard_Deviation[2]
)

a_n <- c(0.7599511, 1.9884051)
term_n <- c(0, 0)
keep_constant <- c(0, 0)
modelform <- "M"
fir <- 0

model_control <- list(
  "basic" = FALSE, "maxstep" = 100,
  "log_bound" = TRUE, "alpha" = 0.05,
  "para_number" = 0, "manual" = TRUE
)
e <- RunCoxRegression_Omnibus(df, t0, t1, event, names,
  term_n = term_n,
  tform = tform, keep_constant = keep_constant,
  a_n = a_n, modelform = modelform, fir = fir,
  control = control, model_control = model_control
)
print("|------------------- Wald Estimate -------------------|")
#> [1] "|------------------- Wald Estimate -------------------|"
print(ci_1)
#> [1] -0.01707914  1.53698136
Interpret_Output(e, 5)
#> |-------------------------------------------------------------------|
#> Likelihood Boundary Results
#> Lower limit converged to at -0.0099 at a score of -107.30968 with of goal of -107.30969
#> Upper limit converged to at 1.55991 at a score of -107.30968 with of goal of -107.30969
#> Run finished in 0.06489 seconds
#> |-------------------------------------------------------------------|

a_n <- c(0.7599511, 1.9884051)
model_control <- list(
  "basic" = FALSE, "maxstep" = 100,
  "log_bound" = TRUE, "alpha" = 0.05,
  "para_number" = 1, "manual" = TRUE
)
e <- RunCoxRegression_Omnibus(df, t0, t1, event, names,
  term_n = term_n,
  tform = tform, keep_constant = keep_constant,
  a_n = a_n, modelform = modelform, fir = fir,
  control = control, model_control = model_control
)
print("|------------------- Likelihood Bound Estimate -------------------|")
#> [1] "|------------------- Likelihood Bound Estimate -------------------|"
print(ci_2)
#> [1] 0.800038 3.176772
Interpret_Output(e, 5)
#> |-------------------------------------------------------------------|
#> Likelihood Boundary Results
#> Lower limit converged to at 0.84124 at a score of -107.30968 with of goal of -107.30969
#> Upper limit converged to at 3.24203 at a score of -107.30968 with of goal of -107.30969
#> Run finished in 0.0654 seconds
#> |-------------------------------------------------------------------|

Next we analyze a model with a linear effect. We would expect the predictions to be further off. The boundaries for temperature are (-0.522, 2.800) and (-0.010, 3.758), and the boundaries for voltage are (0.800, 3.177) and (0.841, 3.242). The estimates for voltage boundary are the same, but the estimates for the temperature boundary are much further off.

names <- c("temperature", "voltage")
tform <- c("plin", "loglin")
ci_1 <- c(
  e2$beta_0[1] - 1.96 * e2$Standard_Deviation[1],
  e2$beta_0[1] + 1.96 * e2$Standard_Deviation[1]
)
ci_2 <- c(
  e2$beta_0[2] - 1.96 * e2$Standard_Deviation[2],
  e2$beta_0[2] + 1.96 * e2$Standard_Deviation[2]
)

a_n <- c(1.138152, 1.988403)
term_n <- c(0, 0)
keep_constant <- c(0, 0)
modelform <- "M"
fir <- 0

model_control <- list(
  "basic" = FALSE, "maxstep" = 100,
  "log_bound" = TRUE, "alpha" = 0.05,
  "para_number" = 0, "manual" = TRUE
)
e <- RunCoxRegression_Omnibus(df, t0, t1, event, names,
  term_n = term_n,
  tform = tform, keep_constant = keep_constant,
  a_n = a_n, modelform = modelform, fir = fir,
  control = control, model_control = model_control
)
print("|------------------- Wald Estimate -------------------|")
#> [1] "|------------------- Wald Estimate -------------------|"
print(ci_1)
#> [1] -0.5232476  2.7995516
Interpret_Output(e, 5)
#> |-------------------------------------------------------------------|
#> Likelihood Boundary Results
#> Lower limit converged to at -0.00984 at a score of -107.30967 with of goal of -107.30969
#> Upper limit converged to at 3.75837 at a score of -107.30968 with of goal of -107.30969
#> Run finished in 0.06429 seconds
#> |-------------------------------------------------------------------|

a_n <- c(1.138152, 1.988403)
model_control <- list(
  "basic" = FALSE, "maxstep" = 100,
  "log_bound" = TRUE, "alpha" = 0.05,
  "para_number" = 1, "manual" = TRUE
)
e <- RunCoxRegression_Omnibus(df, t0, t1, event, names,
  term_n = term_n,
  tform = tform, keep_constant = keep_constant,
  a_n = a_n, modelform = modelform, fir = fir,
  control = control, model_control = model_control
)
print("|------------------- Wald Estimate -------------------|")
#> [1] "|------------------- Wald Estimate -------------------|"
print(ci_2)
#> [1] 0.8000367 3.1767700
Interpret_Output(e, 5)
#> |-------------------------------------------------------------------|
#> Likelihood Boundary Results
#> Lower limit converged to at 0.84124 at a score of -107.30968 with of goal of -107.30969
#> Upper limit converged to at 3.24203 at a score of -107.30968 with of goal of -107.30969
#> Run finished in 0.06227 seconds
#> |-------------------------------------------------------------------|

Illustration of Issues with Likelihood-Boundary Algorithm

One important thing to keep in mind is that the likelihood-based boundary algorithm is not perfect, and at times it may be important to manually solve for the likelihood curve. The following example outlines how this is done and what details about the curve can cause issues for the boundary algorithm. The following uses a dataset used by Colossus for unit testing. The linear parameter was selected for analysis. For each point on a grid, the linear parameter was fixed and the model was optimized.

fname <- "base_example.csv"
df <- fread(fname)

time1 <- "entry"
time2 <- "exit"
event <- "event"
names <- c("dose0", "dose1", "dose0")
term_n <- c(0, 0, 1)
tform <- c("loglin", "loglin", "lin")
keep_constant <- c(0, 0, 1)
a_n <- c(-1.493177, 5.020007, 1.438377)
modelform <- "M"
fir <- 0
der_iden <- 0
#
model_control <- list()
control <- list(
  "ncores" = 2, "lr" = 0.75, "maxiters" = c(100, 100), "halfmax" = 5,
  "epsilon" = 1e-6, "deriv_epsilon" = 1e-6, "abs_max" = 1.0,
  "change_all" = TRUE, "dose_abs_max" = 100.0, "verbose" = 0,
  "ties" = "breslow", "double_step" = 1
)

v0 <- sort(c((0:50 / 50 - 1.0) * 0.8, 1:50 / 50 * 3, 1.438377, -0.5909))
for (v in v0) {
  a_n <- c(-1.493177, 5.020007, v)
  e <- RunCoxRegression_Omnibus(df, time1, time2, event, names,
    term_n = term_n,
    tform = tform, keep_constant = keep_constant, a_n = a_n,
    modelform = modelform, fir = fir, der_iden = der_iden,
    control = control, model_control = model_control
  )
  ll <- e$LogLik
  beta <- e$beta_0
  print(c(ll, beta[3]))
}

What is important to note is that there are two local optimums within a small range (-0.6 and the global solution at 1.4). The algorithms used for solving the likelihood boundary, similar to the standard regression optimizing algorithm, is trapped in local optimums. This means that if the algorithm at any point has to cross over the local optimum, it can be trapped. The two optimums are close enough in score that a 95% confidence interval has a lower boundary below -0.5, but a 50% confidence interval has a lower bound between -0.5 and 1.4. This meant that the algorithm converged to the 50% confidence interval boundary, but failed to converge for the lower boundary of the 95% confidence interval boundary. Development is ongoing to automate the process for solving the complete likelihood curve.

x <- c(-0.8, -0.784, -0.768, -0.752, -0.736, -0.72, -0.704, -0.688, -0.672, -0.656, -0.64, -0.624, -0.608, -0.592, -0.5909, -0.576, -0.56, -0.544, -0.528, -0.512, -0.496, -0.48, -0.464, -0.448, -0.432, -0.416, -0.4, -0.384, -0.368, -0.352, -0.336, -0.32, -0.304, -0.288, -0.272, -0.256, -0.24, -0.224, -0.208, -0.192, -0.176, -0.16, -0.144, -0.128, -0.112, -0.096, -0.08, -0.064, -0.048, -0.032, -0.016, 0.0, 0.06, 0.12, 0.18, 0.24, 0.3, 0.36, 0.42, 0.48, 0.54, 0.6, 0.66, 0.72, 0.78, 0.84, 0.9, 0.96, 1.02, 1.08, 1.14, 1.2, 1.26, 1.32, 1.38, 1.438377, 1.44, 1.5, 1.56, 1.62, 1.68, 1.74, 1.8, 1.86, 1.92, 1.98, 2.04, 2.1, 2.16, 2.22, 2.28, 2.34, 2.4, 2.46, 2.52, 2.58, 2.64, 2.7, 2.76, 2.82, 2.88, 2.94, 3.0)
y <- c(-18500.53, -18499.829, -18499.273, -18498.831, -18498.482, -18498.21, -18497.995, -18497.832, -18497.71, -18497.621, -18497.56, -18497.519, -18497.498, -18497.49, -18497.4904, -18497.495, -18497.51, -18497.53, -18497.558, -18497.589, -18497.624, -18497.66, -18497.7, -18497.739, -18497.779, -18497.818, -18497.86, -18497.896, -18497.933, -18497.969, -18498.003, -18498.04, -18498.067, -18498.096, -18498.124, -18498.15, -18498.17, -18498.196, -18498.216, -18498.235, -18498.252, -18498.27, -18498.281, -18498.292, -18498.303, -18498.311, -18498.32, -18498.324, -18498.329, -18498.332, -18498.334, -18498.33, -18498.33, -18498.31, -18498.27, -18498.23, -18498.18, -18498.13, -18498.07, -18498.01, -18497.96, -18497.9, -18497.84, -18497.78, -18497.73, -18497.68, -18497.63, -18497.59, -18497.56, -18497.52, -18497.49, -18497.47, -18497.45, -18497.44, -18497.43, -18497.429487, -18497.43, -18497.43, -18497.44, -18497.45, -18497.47, -18497.5, -18497.52, -18497.56, -18497.6, -18497.64, -18497.69, -18497.74, -18497.8, -18497.86, -18497.93, -18498.0, -18498.07, -18498.15, -18498.23, -18498.32, -18498.41, -18498.5, -18498.6, -18498.7, -18498.81, -18498.92, -18499.03)

df <- data.table("x" = x, "y" = y)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y)) +
  ggplot2::geom_line(color = "black", alpha = 1, "linewidth" = 1.5) +
  ggplot2::labs(x = "Linear Parameter Value", y = "Log-Likelihood") +
  ggplot2::ggtitle("Multi-Peak Curve")
g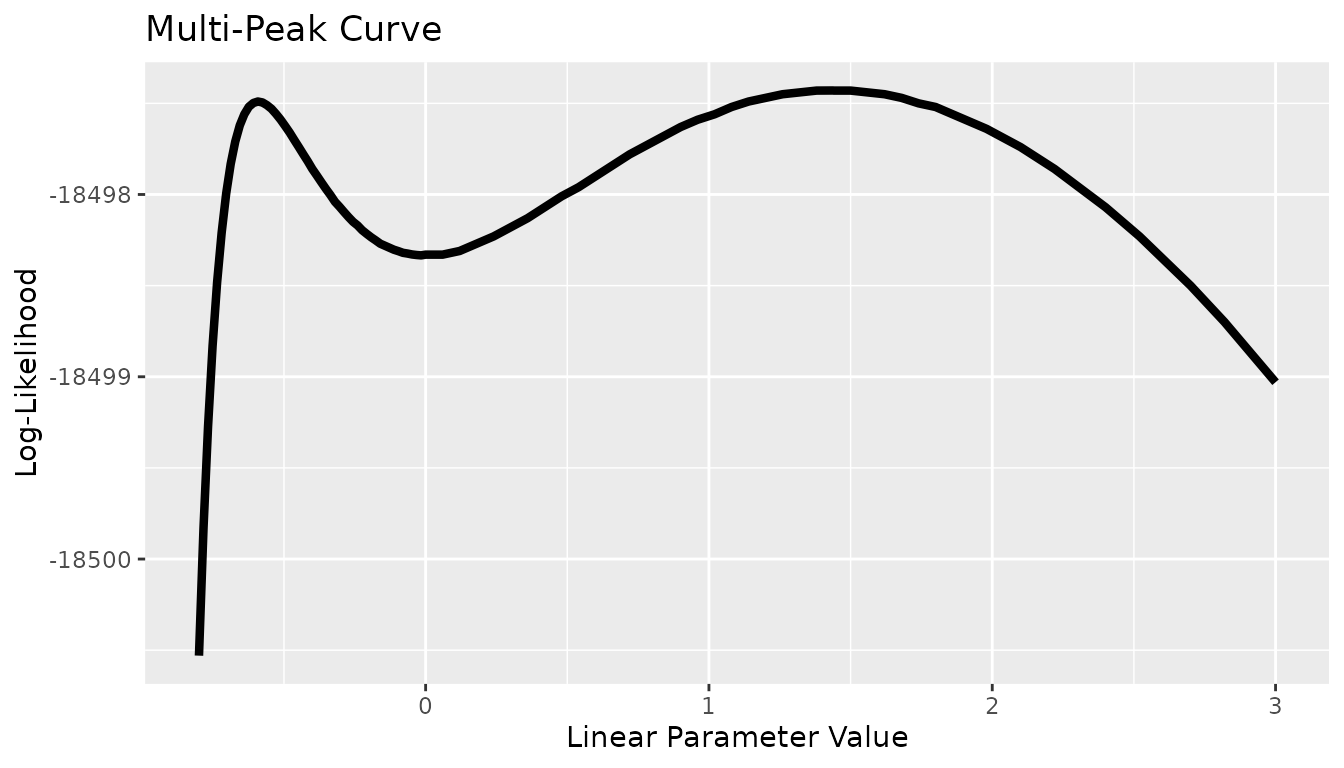

Likelihood Boundary Algorithm Alternative

As an alternative to the likelihood algorithm, a direct curve solving method is implemented. The CoxCurveSolver function solves for the boundary values by iteratively optimizing points and using the bisection method. Each step is approximately as fast as running a single regression. The same model_control options are used to select which parameter is selected and what alpha to use, but adds an additional option “step_size” which is the default search window width used. The bisection method functions by (1) selecting an interval, (2) optimizing at the upper, lower, and midpoint of the interval, and (3) checking if the goal likelihood is crossed. If at-least one of the interval points are on each side of the goal then the interval is narrowed, and if not then the interval is shifted away from the optimum.

fname <- "base_example.csv"
df <- fread(fname)

time1 <- "entry"
time2 <- "exit"
event <- "event"
names <- c("dose0", "dose1", "dose0")
term_n <- c(0, 0, 1)
tform <- c("loglin", "loglin", "lin")
keep_constant <- c(0, 0, 1)
a_n <- c(-1.493177, 5.020007, 1.438377)
modelform <- "M"
fir <- 0
der_iden <- 0
#
model_control <- list()
control <- list(
  "ncores" = 2, "lr" = 0.75, "maxiters" = c(100, 100), "halfmax" = 5,
  "epsilon" = 1e-6, "deriv_epsilon" = 1e-6, "abs_max" = 1.0,
  "change_all" = TRUE, "dose_abs_max" = 100.0, "verbose" = 0,
  "ties" = "breslow", "double_step" = 1
)

model_control <- list("basic" = FALSE, "maxstep" = 20, "log_bound" = FALSE, "alpha" = 0.005, "para_num" = 2, "step_size" = 0.5)
e <- CoxCurveSolver(df, time1, time2, event, names, term_n = term_n, tform = tform, keep_constant = keep_constant, a_n = a_n, modelform = modelform, fir = fir, der_iden = der_iden, control = control, strat_col = "nan", model_control = model_control)

In summary there are three functions available for calculating likelihood based boundaries. The first method is the standard Venzon-Moolgavkar algorithm. This method attempts to both optimize the model and guide the desired parameter to the boundary value. This method is the fastest, but most susceptible to local extrema. Using this algorithm depends on the initial step not being close to a local extrema, so the initial step can be scaled up or down. The second method is a modification of the Venzon-Moolgavkar algorithm. In the second method the initial step is split into multiple guesses, and each guess is optimized independently. The Venzon-Moolgavkar algorithm is then continued at the closest guess that did not exceed the target likelihood. In theory this method makes it more likely for the algorithm to start at an appropriate point, so it is slower but slightly less susceptible to local extrema. However the final portion of the algorithm is still based on derivatives, so it still susceptible to local extrema. The third method is an iterative bisection method. In this algorithm the desired parameter is fixed, and the model is optimized at the endpoints of an interval until an interval is located which contains the goal likelihood. Then the interval is split in half until the interval width is within a user-set limit. This method takes advantage of the fact that the likelihood curve is continuous and we know that the optimum point must be above the goal. The algorithm is split into two steps: optimizing the model at fixed points and determining if the interval contains the goal. The second step does not depend on the likelihood derivatives, so it is not prone to getting stuck in local extrema. However the interval width must be small enough not to step over the solution. Given a small enough interval width, every optimization is likely to converge and the solution is unlikely to be skipped. This method requires the model to be optimized repeatedly, so it is expected to take the longest. However the bisection method is the least likely to have issues converging.