Skip to contents

Gradient and Hessian Approaches

Source: vignettes/Grad_Hess.Rmd
Grad_Hess.Rmd

Optimization Theory

Colossus offers three levels of score calculation, calculating only the score, calculating the score and first derivative, and calculating the score and both first and second derivatives. The second and third options correspond to the Gradient Descent and Newton-Raphson optimization approaches. The goal of this vignette is to discuss how these methods are different, and in what circumstances each might be most appropriate. In both cases the algorithm is designed to iteratively change the parameter estimates to approach a set of parameter values which optimize the score. The major difference is how much information is being calculated and used. The Newton-Raphson algorithm calculates the second derivative matrix, inverts it, and solves a linear system of equations to set the first derivative vector to zero. This method establishes both a magnitude and direction for every step. So every step has several time-intensive calculations, but the new parameter estimates are informed. In this algorithm Colossus uses both a learning rate (η\eta) and maximum allowable parameter change (βmax\beta_{max}).

Δβ×∂2LL∂β2≈−∂LL∂βΔβ=−η∂LL∂βt×(∂2LL∂βt2)−1βt+1=βt+sign(Δβ)*min([|Δβ|,βmax]) \begin{aligned} \Delta \beta \times \frac{\partial^2 LL}{\partial \beta^2} \approx - \frac{\partial LL}{\partial \beta} \\ \Delta \beta = - \eta \frac{\partial LL}{\partial \beta_{t}} \times \left ( \frac{\partial^2 LL}{\partial \beta_{t}^2} \right)^{-1} \\ \beta_{t+1} = \beta_{t} + sign(\Delta \beta)*min \left( \left[ \left|\Delta \beta \right|, \beta_{max} \right] \right) \end{aligned}

The alternative is a Gradient descent approach. In this algorithm, the first derivatives are calculated and used to determine the vector with highest change in score. This establishes a direction for the change in parameters, which is multiplied by the learning rate (η\eta). Similar to the Newton-Raphson algorithm, the magnitude is normalized to the maximum allowable parameter change (βmax\beta_{max}). Colossus uses half-steps to slowly reduce the allowable step size as the solution approaches the optimum. The Gradient algorithm avoids the time-intensive second-derivative calculations, but takes less informed steps. So each iteration runs faster, but more iterations may be required.

Δβ=η*∂LL∂ββt+1=βt+sign(Δβ)*min([|Δβ|,βmax]) \begin{aligned} \Delta \beta = \eta * \frac{\partial LL}{\partial \beta}\\ \beta_{t+1} = \beta_{t} + sign(\Delta \beta)*min \left( \left[ \left|\Delta \beta \right|, \beta_{max} \right] \right) \end{aligned}

The standard half-step framework is not likely to be sufficient for the Gradient descent algorithm. Because of this, several different optimization options have been or will be added, like momentum, adadelta, and adam, which use previous information about the gradient to inform the step size for future steps. The first method, momentum, applies a weighted sum (γ\gamma) of the current and previous step. This is done to speed up steps moving toward the optimum position and correct for when the algorithm oversteps. This can avoid the issue of oscillation around an optimum value.

Δβt=γ*Δβt−1+η*∂LL∂ββt+1=βt+sign(Δβt)*min([|Δβt|,βmax]) \begin{aligned} \Delta \beta_{t} = \gamma * \Delta \beta_{t-1} + \eta * \frac{\partial LL}{\partial \beta}\\ \beta_{t+1} = \beta_{t} + sign(\Delta \beta_{t})*min \left( \left[ \left|\Delta \beta_{t} \right|, \beta_{max} \right] \right) \end{aligned}

The next method, the adadelta method, applies a parameter specific learning rate by tracking the root mean square (RMS) gradient and parameter updates within a window. Instead of tracking a true window of iteration, the old estimate of RMS is decayed by a weight (γ\gamma) before being added to the new estimate. The ratio of RMS parameter update to RMS gradient is used to normalize the results back in the correct units. A small offset (ϵ\epsilon) is used to avoid the case of division by zero.

gt=(∂LL∂β)tE[g2]t=γ*E[g2]t−1+(1−γ)*gt2E[Δβ2]t−1=γ*E[Δβ2]t−2+(1−γ)*Δβt−12RMS[g]t=E[g2]t+ϵRMS[Δβ]t−1=E[Δβ2]t−1+ϵΔβt=RMS[Δβ]t−1RMS[g]t*gtβt+1=βt+sign(Δβt)*min([|Δβt|,βmax]) \begin{aligned} g_t = \left (\frac{\partial LL}{\partial \beta} \right)_{t} \\ E[g^2]_{t} = \gamma * E[g^2]_{t-1} + (1-\gamma) * g^2_{t} \\ E[\Delta \beta^2]_{t-1} = \gamma * E[\Delta \beta^2]_{t-2} + (1-\gamma) * \Delta \beta^2_{t-1} \\ RMS[g]_t = \sqrt{E[g^2]_{t} + \epsilon} \\ RMS[\Delta \beta]_{t-1} = \sqrt{E[\Delta \beta^2]_{t-1} + \epsilon} \\ \Delta \beta_{t} = \frac{RMS[\Delta \beta]_{t-1}}{RMS[g]_t} * g_t\\ \beta_{t+1} = \beta_{t} + sign(\Delta \beta_{t})*min \left( \left[ \left|\Delta \beta_{t} \right|, \beta_{max} \right] \right) \end{aligned}

The final method, adam, combines the theory behind the momentum and adadelta methods. The adam method tracks an estimate of the first moment vector (mm) and second moment vector (vv), which are weighted by decay parameters (β1,β2\beta_1, \beta_2). These are bias corrected to correct for bias in early iterations (m̂,v̂\hat{m}, \hat{v}). The learning rate (η\eta) and second moment vector provide the decaying learning rate from adadelta, and the first moment vector provides an effect similar to momentum. Combined these have generally been able to stabilize gradient descent algorithms without incurring a significant computational cost.

gt=(∂LL∂β)tm0,v0=0,0mt=β1*mt−1+(1−β1)*gtvt=β2*vt−1+(1−β2)*gt2m̂t=mt/(1−β1t)v̂t=vt/(1−β2t)Δβt=ηv̂t+ϵ*m̂tβt+1=βt+sign(Δβt)*min([|Δβt|,βmax]) \begin{aligned} g_t = \left (\frac{\partial LL}{\partial \beta} \right)_{t} \\ m_0, v_0 = 0, 0 \\ m_t = \beta_1 * m_{t-1} + (1-\beta_1) * g_t \\ v_t = \beta_2 * v_{t-1} + (1-\beta_2) * g^2_t \\ \hat{m}_t = m_t / (1-\beta_1^t) \\ \hat{v}_t = v_t / (1-\beta_2^t) \\ \Delta \beta_{t} = \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} * \hat{m}_t \\ \beta_{t+1} = \beta_{t} + sign(\Delta \beta_{t})*min \left( \left[ \left|\Delta \beta_{t} \right|, \beta_{max} \right] \right) \end{aligned}

Use in Practice

The first thing to acknowledge is that the gradient descent method may require more hyperparameter tuning than the standard Newton-Raphson method. In general it may be necessary to run the analysis multiple times with different learning rates, decay terms, and offset. The following test example shows the basic usage for a simple model.

fname <- "tests/testthat/ll_comp_0.csv"
colTypes <- c("double", "double", "double", "integer", "integer")
df <- fread(fname, nThread = min(c(detectCores(), 2)), data.table = TRUE, header = TRUE, colClasses = colTypes, verbose = FALSE, fill = TRUE)
set.seed(3742)
df$rand <- floor(runif(nrow(df), min = 0, max = 5))
time1 <- "t0"
time2 <- "t1"
modelform <- "M"
fir <- 0
der_iden <- 0
event <- "lung"
a_n <- c(-0.1, -0.1)
keep_constant <- c(0, 0)

for (method in c("momentum", "adadelta", "adam", "gradient")) {
  model_control <- list("gradient" = TRUE, "epsilon_decay" = 1e-4)
  model_control[[method]] <- TRUE
  a_n <- c(-0.1, -0.1)
  control <- list("ncores" = 2, "lr" = 0.2, "maxiters" = c(1, 20), "halfmax" = 2, "epsilon" = 1e-6, "deriv_epsilon" = 1e-6, "abs_max" = 1.0, "change_all" = TRUE, "dose_abs_max" = 100.0, "verbose" = 4, "ties" = "breslow", "double_step" = 1)
  modelform <- "M"
  e <- RunCoxRegression_Omnibus(df, time1, time2, event, names, term_n = term_n, tform = tform, keep_constant = keep_constant, a_n = a_n, modelform = modelform, fir = fir, der_iden = der_iden, control = control, strat_col = "rand", model_control = model_control, cens_weight = "weighting")
  Interpret_Output(e)
}
x <- c(
  -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.95, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.9, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.85, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.75, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.7, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.65, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.55, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.45, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.35, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.3, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.25, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.15, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.1, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, -0.05, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.3, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.35, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.45, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.55, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.65, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.9, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 0.95, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
)
y <- c(
  -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0, -1.0, -0.95, -0.9, -0.85, -0.8, -0.75, -0.7, -0.65, -0.6, -0.55, -0.5, -0.45, -0.4, -0.35, -0.3, -0.25, -0.2, -0.15, -0.1, -0.05, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0
)
c <- c(
  264.6882, 264.033, 263.4076, 262.8126, 262.2482, 261.7146, 261.2122, 260.741, 260.3016, 259.894, 259.5182, 259.1744, 258.8626, 258.583, 258.3354, 258.1196, 257.9358, 257.7838, 257.6634, 257.5742, 257.5162, 257.489, 257.4924, 257.526, 257.5894, 257.682, 257.8038, 257.954, 258.1324, 258.3382, 258.571, 258.8304, 259.1156, 259.4264, 259.7618, 260.1214, 260.5048, 260.911, 261.3398, 261.7902, 262.2618, 263.5038, 262.8408, 262.2076, 261.6046, 261.0322, 260.4904, 259.98, 259.5008, 259.0532, 258.6374, 258.2534, 257.9016, 257.5818, 257.294, 257.0382, 256.8146, 256.623, 256.463, 256.3348, 256.238, 256.1724, 256.1378, 256.1338, 256.16, 256.2162, 256.302, 256.4168, 256.5602, 256.7318, 256.9312, 257.1578, 257.411, 257.6902, 257.995, 258.3246, 258.6788, 259.0566, 259.4576, 259.8812, 260.3266, 260.7936, 262.3582, 261.6874, 261.0464, 260.4356, 259.855, 259.3054, 258.7868, 258.2996, 257.844, 257.42, 257.028, 256.668, 256.34, 256.0442, 255.7806, 255.549, 255.3494, 255.1816, 255.0456, 254.9412, 254.868, 254.8258, 254.8144, 254.8334, 254.8824, 254.961, 255.069, 255.2056, 255.3706, 255.5634, 255.7836, 256.0306, 256.3038, 256.6026, 256.9266, 257.275, 257.6474, 258.043, 258.4614, 258.902, 259.364, 261.2514, 260.573, 259.9242, 259.3054, 258.7172, 258.1596, 257.633, 257.1378, 256.674, 256.242, 255.842, 255.4738, 255.1378, 254.834, 254.5624, 254.3228, 254.1154, 253.9398, 253.796, 253.6838, 253.603, 253.5534, 253.5346, 253.5462, 253.588, 253.6596, 253.7606, 253.8904, 254.0488, 254.2352, 254.4488, 254.6896, 254.9566, 255.2496, 255.5676, 255.9104, 256.2774, 256.6678, 257.081, 257.5164, 257.9736, 260.1838, 259.4978, 258.8414, 258.2148, 257.6186, 257.0532, 256.5186, 256.0154, 255.5436, 255.1036, 254.6956, 254.3194, 253.9754, 253.6636, 253.384, 253.1364, 252.921, 252.7378, 252.5862, 252.4664, 252.378, 252.3208, 252.2946, 252.2988, 252.3336, 252.398, 252.492, 252.6152, 252.7668, 252.9464, 253.1538, 253.3882, 253.6492, 253.936, 254.2484, 254.5856, 254.9468, 255.3318, 255.7398, 256.1702, 256.6226, 259.1556, 258.462, 257.7978, 257.1636, 256.5596, 255.9864, 255.444, 254.9328, 254.4532, 254.0052, 253.589, 253.205, 252.853, 252.5332, 252.2456, 251.9902, 251.767, 251.5758, 251.4164, 251.289, 251.193, 251.1282, 251.0946, 251.0916, 251.119, 251.1766, 251.2636, 251.3798, 251.5248, 251.6978, 251.8988, 252.1268, 252.3816, 252.6626, 252.969, 253.3004, 253.6562, 254.0358, 254.4386, 254.8638, 255.3112, 258.1668, 257.4658, 256.7942, 256.1522, 255.5406, 254.9594, 254.4092, 253.8902, 253.4026, 252.9466, 252.5226, 252.1306, 251.7706, 251.443, 251.1474, 250.8842, 250.653, 250.454, 250.287, 250.1518, 250.0482, 249.976, 249.935, 249.9248, 249.945, 249.9954, 250.0754, 250.1848, 250.323, 250.4896, 250.684, 250.9058, 251.1544, 251.4292, 251.7298, 252.0554, 252.4056, 252.7798, 253.1774, 253.5976, 254.0398, 257.2178, 256.5094, 255.8302, 255.1808, 254.5614, 253.9726, 253.4146, 252.8878, 252.3924, 251.9286, 251.4966, 251.0966, 250.7288, 250.3932, 250.0898, 249.8186, 249.5798, 249.373, 249.1982, 249.0554, 248.9442, 248.8646, 248.816, 248.7984, 248.8114, 248.8548, 248.9278, 249.0302, 249.1618, 249.3218, 249.5096, 249.7252, 249.9676, 250.2364, 250.531, 250.851, 251.1956, 251.5642, 251.9564, 252.3714, 252.8088, 256.3088, 255.593, 254.9064, 254.2494, 253.6226, 253.026, 252.4604, 251.9258, 251.4226, 250.9508, 250.511, 250.1032, 249.7276, 249.384, 249.0728, 248.7938, 248.5472, 248.3326, 248.1502, 247.9996, 247.881, 247.7938, 247.738, 247.713, 247.7188, 247.755, 247.821, 247.9166, 248.0414, 248.1948, 248.3762, 248.5852, 248.8214, 249.0842, 249.373, 249.6872, 250.0262, 250.3894, 250.7762, 251.186, 251.6182, 255.4398, 254.7166, 254.0228, 253.3584, 252.724, 252.12, 251.5466, 251.0044, 250.4934, 250.014, 249.5664, 249.1506, 248.7672, 248.4158, 248.0968, 247.81, 247.5556, 247.3332, 247.1432, 246.985, 246.8588, 246.7642, 246.7008, 246.6688, 246.6674, 246.6964, 246.7554, 246.8442, 246.9622, 247.1088, 247.2838, 247.4866, 247.7166, 247.9732, 248.256, 248.5644, 248.8976, 249.2554, 249.6368, 250.0416, 250.4688, 254.611, 253.8808, 253.1796, 252.5078, 251.866, 251.2544, 250.6736, 250.1236, 249.605, 249.1178, 248.6624, 248.239, 247.8478, 247.4886, 247.1618, 246.8674, 246.6052, 246.3752, 246.1774, 246.0118, 245.878, 245.7758, 245.7052, 245.6658, 245.6572, 245.679, 245.7312, 245.813, 245.9242, 246.0644, 246.2328, 246.4292, 246.6528, 246.9034, 247.1802, 247.4828, 247.8106, 248.1626, 248.5388, 248.9382, 249.3604, 253.8226, 253.0852, 252.377, 251.698, 251.0488, 250.4298, 249.8414, 249.2838, 248.7576, 248.2628, 247.7998, 247.3686, 246.9696, 246.6028, 246.2682, 245.966, 245.6962, 245.4586, 245.2532, 245.08, 244.9386, 244.8292, 244.7512, 244.7044, 244.6886, 244.7034, 244.7486, 244.8236, 244.928, 245.0614, 245.2234, 245.4134, 245.6308, 245.8754, 246.1462, 246.443, 246.765, 247.1116, 247.4824, 247.8764, 248.2936, 253.0748, 252.3304, 251.615, 250.9288, 250.2724, 249.646, 249.0502, 248.4852, 247.9514, 247.4492, 246.9784, 246.5396, 246.133, 245.7584, 245.4162, 245.1064, 244.8288, 244.5836, 244.3708, 244.19, 244.0412, 243.9242, 243.8388, 243.7848, 243.762, 243.7696, 243.8078, 243.876, 243.9736, 244.1004, 244.256, 244.4396, 244.6508, 244.8892, 245.154, 245.4448, 245.7612, 246.1024, 246.4676, 246.8566, 247.2686, 252.3676, 251.6164, 250.894, 250.2006, 249.537, 248.9034, 248.3004, 247.728, 247.1866, 246.6768, 246.1986, 245.7522, 245.338, 244.9558, 244.606, 244.2884, 244.0034, 243.7506, 243.5302, 243.3418, 243.1856, 243.0614, 242.9686, 242.9074, 242.8774, 242.878, 242.9092, 242.9706, 243.0614, 243.1816, 243.3306, 243.5078, 243.7128, 243.945, 244.204, 244.489, 244.7996, 245.1352, 245.4952, 245.8788, 246.2856, 251.7014, 250.9434, 250.214, 249.5136, 248.843, 248.2022, 247.5918, 247.012, 246.4634, 245.946, 245.4604, 245.0064, 244.5846, 244.195, 243.8376, 243.5126, 243.2198, 242.9596, 242.7316, 242.536, 242.3724, 242.2406, 242.1408, 242.0722, 242.035, 242.0288, 242.053, 242.1074, 242.1916, 242.3052, 242.4478, 242.6186, 242.8174, 243.0434, 243.2964, 243.5756, 243.8806, 244.2106, 244.565, 244.9434, 245.3452, 251.076, 250.3112, 249.575, 248.8678, 248.19, 247.5422, 246.9246, 246.3376, 245.7818, 245.257, 244.764, 244.3026, 243.8734, 243.4762, 243.1114, 242.7788, 242.4786, 242.2108, 241.9754, 241.7724, 241.6014, 241.4624, 241.3552, 241.2796, 241.2354, 241.222, 241.2394, 241.287, 241.3646, 241.4716, 241.6076, 241.772, 241.9646, 242.1846, 242.4316, 242.705, 243.0042, 243.3286, 243.6778, 244.0508, 244.4474, 250.4916, 249.7204, 248.9774, 248.2634, 247.5788, 246.9238, 246.2992, 245.705, 245.1418, 244.61, 244.1096, 243.6408, 243.2042, 242.7996, 242.4272, 242.0874, 241.7798, 241.5046, 241.2618, 241.0514, 240.8732, 240.727, 240.6126, 240.5298, 240.4784, 240.4582, 240.4686, 240.5096, 240.5804, 240.6808, 240.8104, 240.9684, 241.1548, 241.3688, 241.6098, 241.8774, 242.1708, 242.4898, 242.8334, 243.2014, 243.5928, 249.9484, 249.1706, 248.421, 247.7004, 247.0088, 246.347, 245.7154, 245.1142, 244.544, 244.0048, 243.4972, 243.0212, 242.5772, 242.1654, 241.7858, 241.4384, 241.1234, 240.841, 240.591, 240.3732, 240.1876, 240.0342, 239.9128, 239.823, 239.7646, 239.7374, 239.741, 239.7752, 239.8394, 239.9332, 240.0564, 240.2082, 240.3882, 240.5962, 240.8312, 241.093, 241.3808, 241.6942, 242.0326, 242.3952, 242.7814, 249.4464, 248.6622, 247.9062, 247.1788, 246.4806, 245.812, 245.1736, 244.5654, 243.988, 243.4418, 242.927, 242.444, 241.9928, 241.5736, 241.1866, 240.8322, 240.51, 240.2202, 239.9628, 239.7378, 239.5452, 239.3846, 239.256, 239.1592, 239.094, 239.0598, 239.0568, 239.0842, 239.1418, 239.229, 239.3458, 239.4914, 239.6654, 239.8672, 240.0964, 240.3522, 240.6344, 240.9424, 241.2752, 241.6326, 242.0138, 248.9858, 248.1952, 247.4328, 246.699, 245.9942, 245.3188, 244.6736, 244.0586, 243.4744, 242.9212, 242.3994, 241.9092, 241.4508, 241.0244, 240.6304, 240.2686, 239.9392, 239.6424, 239.3778, 239.1458, 238.946, 238.7782, 238.6426, 238.539, 238.4668, 238.4258, 238.416, 238.4366, 238.4876, 238.5686, 238.679, 238.8182, 238.9862, 239.182, 239.4052, 239.6554, 239.932, 240.2344, 240.5618, 240.914, 241.29, 248.5664, 247.7698, 247.001, 246.2608, 245.5494, 244.8676, 244.2156, 243.5938, 243.0028, 242.4428, 241.914, 241.4168, 240.9514, 240.518, 240.1168, 239.748, 239.4116, 239.1076, 238.836, 238.5968, 238.39, 238.2154, 238.0728, 237.9622, 237.8832, 237.8354, 237.8188, 237.833, 237.8776, 237.952, 238.056, 238.1892, 238.351, 238.5408, 238.7582, 239.0026, 239.2736, 239.5706, 239.8928, 240.2396, 240.6106, 248.1884, 247.3856, 246.6108, 245.8642, 245.1466, 244.4582, 243.7998, 243.1714, 242.5736, 242.0068, 241.4712, 240.9672, 240.4948, 240.0546, 239.6464, 239.2706, 238.927, 238.616, 238.3374, 238.0914, 237.8776, 237.696, 237.5466, 237.429, 237.3434, 237.289, 237.2658, 237.2734, 237.3114, 237.3796, 237.4774, 237.6044, 237.76, 237.944, 238.1556, 238.3944, 238.6598, 238.9512, 239.268, 239.6098, 239.9758, 247.8518, 247.0432, 246.2622, 245.5096, 244.7856, 244.091, 243.426, 242.7912, 242.1868, 241.6132, 241.071, 240.5602, 240.081, 239.6338, 239.2188, 238.8362, 238.4858, 238.1678, 237.8824, 237.6294, 237.4088, 237.2204, 237.0642, 236.94, 236.8474, 236.7866, 236.7568, 236.758, 236.7896, 236.8514, 236.943, 237.064, 237.2136, 237.3918, 237.5976, 237.8308, 238.0906, 238.3766, 238.6882, 239.0248, 239.3858, 247.5568, 246.7422, 245.9552, 245.1966, 244.4666, 243.7656, 243.0944, 242.4532, 241.8424, 241.2624, 240.7134, 240.196, 239.7102, 239.2564, 238.8346, 238.445, 238.0878, 237.7632, 237.4708, 237.211, 236.9838, 236.7886, 236.6258, 236.4948, 236.3958, 236.3284, 236.2922, 236.2868, 236.3122, 236.368, 236.4534, 236.5682, 236.712, 236.8842, 237.0844, 237.312, 237.5664, 237.847, 238.1534, 238.485, 238.841, 247.303, 246.4826, 245.69, 244.9254, 244.1894, 243.4824, 242.805, 242.1576, 241.5404, 240.954, 240.3986, 239.8746, 239.3822, 238.9218, 238.4934, 238.0972, 237.7334, 237.402, 237.103, 236.8366, 236.6026, 236.4008, 236.2314, 236.094, 235.9884, 235.9146, 235.872, 235.8604, 235.8796, 235.929, 236.0084, 236.1174, 236.2554, 236.4218, 236.6164, 236.8384, 237.0874, 237.3628, 237.664, 237.9904, 238.3416, 247.0904, 246.2648, 245.4664, 244.696, 243.9542, 243.2412, 242.5578, 241.9042, 241.2808, 240.6882, 240.1264, 239.5962, 239.0974, 238.6304, 238.1956, 237.7928, 237.4224, 237.0846, 236.779, 236.506, 236.2654, 236.0572, 235.8814, 235.7374, 235.6256, 235.5452, 235.4964, 235.4786, 235.4918, 235.5352, 235.6086, 235.7116, 235.8438, 236.0046, 236.1936, 236.4102, 236.6538, 236.924, 237.22, 237.5416, 237.8878, 246.9194, 246.0882, 245.2844, 244.5084, 243.7608, 243.0422, 242.3528, 241.6932, 241.0638, 240.465, 239.8972, 239.3606, 238.8554, 238.3822, 237.941, 237.5318, 237.155, 236.8108, 236.4988, 236.2194, 235.9724, 235.7578, 235.5756, 235.4254, 235.3072, 235.2206, 235.1656, 235.1418, 235.1488, 235.1864, 235.2538, 235.3512, 235.4776, 235.6328, 235.8164, 236.0274, 236.2658, 236.5308, 236.822, 237.1386, 237.48, 246.7896, 245.953, 245.1438, 244.3624, 243.6094, 242.885, 242.1898, 241.5244, 240.8892, 240.2844, 239.7106, 239.1678, 238.6566, 238.1772, 237.7296, 237.3144, 236.9314, 236.5806, 236.2624, 235.9768, 235.7236, 235.5028, 235.3142, 235.1578, 235.0334, 234.9408, 234.8798, 234.85, 234.851, 234.8826, 234.9446, 235.036, 235.157, 235.3066, 235.4848, 235.6906, 235.9238, 236.1838, 236.47, 236.7816, 237.1184, 246.7008, 245.8594, 245.0448, 244.2582, 243.4996, 242.7698, 242.069, 241.398, 240.757, 240.1464, 239.5666, 239.018, 238.5008, 238.0154, 237.5618, 237.1404, 236.7512, 236.3944, 236.07, 235.7782, 235.5188, 235.292, 235.0974, 234.9348, 234.8044, 234.706, 234.639, 234.6032, 234.5986, 234.6244, 234.6806, 234.7666, 234.882, 235.0264, 235.1992, 235.3998, 235.628, 235.8828, 236.1642, 236.471, 236.803, 246.6532, 245.8068, 244.9874, 244.1954, 243.4316, 242.6964, 241.9902, 241.3138, 240.6672, 240.0508, 239.4654, 238.911, 238.388, 237.8966, 237.4372, 237.0098, 236.6148, 236.252, 235.9216, 235.6238, 235.3584, 235.1256, 234.925, 234.7566, 234.6204, 234.516, 234.4432, 234.4018, 234.3914, 234.4116, 234.4622, 234.5428, 234.6528, 234.792, 234.9596, 235.1552, 235.3782, 235.6282, 235.9048, 236.207, 236.5344, 246.6466, 245.7954, 244.971, 244.1742, 243.4052, 242.6648, 241.9534, 241.2716, 240.6196, 239.9978, 239.4068, 238.8468, 238.3182, 237.8212, 237.356, 236.9228, 236.5218, 236.1534, 235.8172, 235.5136, 235.2424, 235.0036, 234.7972, 234.6232, 234.4812, 234.371, 234.2926, 234.2456, 234.2296, 234.2444, 234.2898, 234.365, 234.4698, 234.6036, 234.766, 234.9568, 235.175, 235.4202, 235.692, 235.9896, 236.3126, 246.681, 245.825, 244.996, 244.1942, 243.4204, 242.675, 241.9586, 241.2714, 240.6142, 239.9872, 239.3908, 238.8254, 238.2912, 237.7886, 237.318, 236.8792, 236.4726, 236.0984, 235.7566, 235.4474, 235.1704, 234.9262, 234.7142, 234.5344, 234.3868, 234.2712, 234.1872, 234.1348, 234.1134, 234.123, 234.163, 234.233, 234.3326, 234.4614, 234.619, 234.8048, 235.0182, 235.2588, 235.526, 235.8192, 236.138, 246.756, 245.8956, 245.0618, 244.2554, 243.477, 242.7268, 242.0054, 241.3134, 240.651, 240.0188, 239.4172, 238.8466, 238.3072, 237.7992, 237.323, 236.879, 236.467, 236.0872, 235.74, 235.4252, 235.1428, 234.893, 234.6756, 234.4904, 234.3374, 234.2164, 234.1272, 234.0694, 234.0428, 234.0472, 234.082, 234.147, 234.2416, 234.3656, 234.5184, 234.6994, 234.9082, 235.1442, 235.407, 235.6958, 236.0102, 246.8714, 246.0068, 245.1688, 244.3578, 243.5748, 242.8198, 242.0938, 241.397, 240.7298, 240.0926, 239.486, 238.9104, 238.3658, 237.8526, 237.3714, 236.922, 236.5048, 236.1198, 235.7672, 235.4472, 235.1596, 234.9044, 234.6816, 234.4912, 234.333, 234.2068, 234.1124, 234.0494, 234.0178, 234.017, 234.047, 234.107, 234.197, 234.3162, 234.4642, 234.6406, 234.845, 235.0766, 235.335, 235.6196, 235.93, 247.0274, 246.1586, 245.3162, 244.5012, 243.7136, 242.9544, 242.2236, 241.5222, 240.8504, 240.2084, 239.597, 239.0164, 238.467, 237.949, 237.4626, 237.0082, 236.586, 236.1958, 235.8382, 235.513, 235.2204, 234.96, 234.7322, 234.5368, 234.3734, 234.2422, 234.1428, 234.075, 234.0384, 234.0328, 234.058, 234.1132, 234.1984, 234.313, 234.4566, 234.6286, 234.8286, 235.056, 235.3102, 235.5906, 235.897, 247.2234, 246.3506, 245.5044, 244.6852, 243.8934, 243.1298, 242.3948, 241.689, 241.0126, 240.3662, 239.7502, 239.165, 238.6108, 238.088, 237.5968, 237.1376, 236.7104, 236.3154, 235.953, 235.6228, 235.3252, 235.06, 234.8272, 234.627, 234.4588, 234.3226, 234.2184, 234.1458, 234.1046, 234.0944, 234.1148, 234.1656, 234.2462, 234.3564, 234.4956, 234.6634, 234.859, 235.0824, 235.3324, 235.609, 235.9114, 247.4596, 246.583, 245.7328, 244.9096, 244.114, 243.3464, 242.6072, 241.897, 241.2164, 240.5656, 239.9452, 239.3556, 238.7968, 238.2694, 237.7738, 237.3098, 236.878, 236.4784, 236.1112, 235.7764, 235.474, 235.2042, 234.9668, 234.7616, 234.5888, 234.4482, 234.3392, 234.262, 234.2162, 234.2016, 234.2176, 234.264, 234.3404, 234.4462, 234.5812, 234.7448, 234.9366, 235.1558, 235.402, 235.6748, 235.9734, 247.7354, 246.8552, 246.0014, 245.1746, 244.375, 243.6034, 242.8604, 242.1462, 241.4616, 240.8066, 240.182, 239.588, 239.025, 238.4934, 237.9932, 237.525, 237.0888, 236.6846, 236.313, 235.9736, 235.6668, 235.3924, 235.1506, 234.941, 234.7636, 234.6186, 234.5052, 234.4236, 234.3736, 234.3544, 234.3662, 234.4084, 234.4806, 234.5824, 234.7134, 234.873, 235.0608, 235.2764, 235.5188, 235.788, 236.083, 248.0508, 247.1672, 246.31, 245.4796, 244.6764, 243.9012, 243.1544, 242.4364, 241.7478, 241.089, 240.4604, 239.8624, 239.2952, 238.7594, 238.2552, 237.7828, 237.3422, 236.934, 236.558, 236.2144, 235.9032, 235.6246, 235.3784, 235.1646, 234.983, 234.8336, 234.7162, 234.6304, 234.5762, 234.553, 234.5608, 234.599, 234.6672, 234.765, 234.8922, 235.048, 235.2322, 235.444, 235.6828, 235.9484, 236.2402, 248.4054, 247.5186, 246.6582, 245.8244, 245.0178, 244.2392, 243.4888, 242.7672, 242.075, 241.4124, 240.78, 240.1782, 239.6072, 239.0676, 238.5594, 238.0828, 237.6384, 237.2262, 236.846, 236.4984, 236.1834, 235.9006, 235.6504, 235.4326, 235.247, 235.0934, 234.972, 234.8824, 234.824, 234.797, 234.801, 234.8352, 234.8998, 234.994, 235.1174, 235.2696, 235.4502, 235.6586, 235.8942, 236.1564, 236.4448, 248.799, 247.9094, 247.0458, 246.2088, 245.399, 244.617, 243.8634, 243.1384, 242.4428, 241.7768, 241.1408, 240.5354, 239.9608, 239.4174, 238.9056, 238.4254, 237.977, 237.561, 237.1772, 236.8258, 236.5068, 236.2202, 235.9662, 235.7444, 235.555, 235.3978, 235.2726, 235.1792, 235.1172, 235.0864, 235.0866, 235.1174, 235.1784, 235.269, 235.389, 235.5378, 235.715, 235.9202, 236.1524, 236.4116, 236.6968
)
dft <- data.table("x" = x, "y" = y, "Score" = c)
g <- ggplot2::ggplot() +
  ggplot2::geom_point(data = dft, ggplot2::aes(
    x = .data$x, y = .data$y,
    color = .data$Score
  ), size = 2) +
  ggplot2::scale_fill_continuous(guide = ggplot2::guide_colourbar(title = "-2*Log-Likelihood")) +
  ggplot2::xlab("Parameter 1") +
  ggplot2::ylab("Parameter 2") +
  ggplot2::ggtitle("-2*Log-Likelihood") +
  ggplot2::scale_colour_viridis_c()
g

Every gradient descent algorithm available was tested at the same starting point. In all cases the algorithm approaches the solution, at different rates. In this case there are no local extrema, so the standard approach is fine. These show some fundamental differences between the methods. The effect of momentum is clearly visible compared to the standard option, the estimates do not oscillate as quickly. The differences between adadelta and adam is also visible, the adam method is able to converge quicker. These results are not necessarily using optimized hyperparameters however. This is not meant to prove which method was the best.

x <- c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)
y <- c(-0.1, 0.9, 0.446528, 0.839821, 0.493552, 0.799313, 0.528609, 0.768118, 0.555872, 0.743827, 0.577191, 0.724839, 0.593904, 0.70996, 0.607026, 0.698284, 0.617337, 0.689114, 0.625445, 0.681907, 0.631822, 0.67624, 0.67624, -0.1, 0.9, 0.446528, 0.431696, 0.834161, 0.857333, 0.501858, 0.477865, 0.793264, 0.814217, 0.531039, 0.511871, 0.770217, 0.78877, 0.55277, 0.530413, 0.745479, 0.771659, 0.578773, 0.54938, 0.72037, 0.750178, 0.750178, -0.1, -0.0683777, -0.0236573, 0.0204036, 0.0631351, 0.104199, 0.143407, 0.180661, 0.215914, 0.249159, 0.280419, 0.309735, 0.337162, 0.362769, 0.386631, 0.408828, 0.429444, 0.448562, 0.466269, 0.482647, 0.497779, 0.511745, 0.511745, -0.1, 0.0999967, 0.299992, 0.49416, 0.672686, 0.818272, 0.912721, 0.951325, 0.943139, 0.900966, 0.836339, 0.759197, 0.678706, 0.6037, 0.542181, 0.50002, 0.479848, 0.481022, 0.500511, 0.53392, 0.576232, 0.622276, 0.622276)
c <- c("standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam")

df <- data.table("x" = x, "y" = y, "method" = c)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y, group = .data$method, color = .data$method)) +
  ggplot2::geom_line("linewidth" = 1.2) +
  ggplot2::labs(x = "Iteration", y = "First Parameter Value") +
  ggplot2::ggtitle("First Parameter Value Convergence")
g

x <- c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)
y <- c(-0.1, 0.382267, 0.481728, 0.371577, 0.474396, 0.383262, 0.464408, 0.392812, 0.456452, 0.40023, 0.45019, 0.406007, 0.445259, 0.41052, 0.441374, 0.414052, 0.438314, 0.416821, 0.435902, 0.418993, 0.434002, 0.420699, 0.420699, -0.1, 0.382267, 0.481728, 0.461092, 0.353981, 0.381487, 0.499642, 0.486223, 0.365388, 0.35904, 0.467404, 0.490215, 0.404434, 0.37681, 0.439266, 0.459563, 0.412495, 0.405195, 0.44752, 0.445014, 0.399118, 0.404763, 0.404763, -0.1, -0.0683799, -0.0236649, 0.0193058, 0.0594837, 0.0964731, 0.130195, 0.160739, 0.188284, 0.213051, 0.235278, 0.255201, 0.273049, 0.289032, 0.303346, 0.316169, 0.327659, 0.337961, 0.347201, 0.355493, 0.36294, 0.36963, 0.36963, -0.1, 0.0999917, 0.299977, 0.469249, 0.559129, 0.571139, 0.537754, 0.485171, 0.434002, 0.399975, 0.38974, 0.400107, 0.422011, 0.444253, 0.456706, 0.453734, 0.435816, 0.40853, 0.380544, 0.36118, 0.357234, 0.370462, 0.370462)
c <- c("standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam")

df <- data.table("x" = x, "y" = y, "method" = c)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y, group = .data$method, color = .data$method)) +
  ggplot2::geom_line("linewidth" = 1.2) +
  ggplot2::labs(x = "Iteration", y = "Second Parameter Value") +
  ggplot2::ggtitle("Second Parameter Value Convergence")
g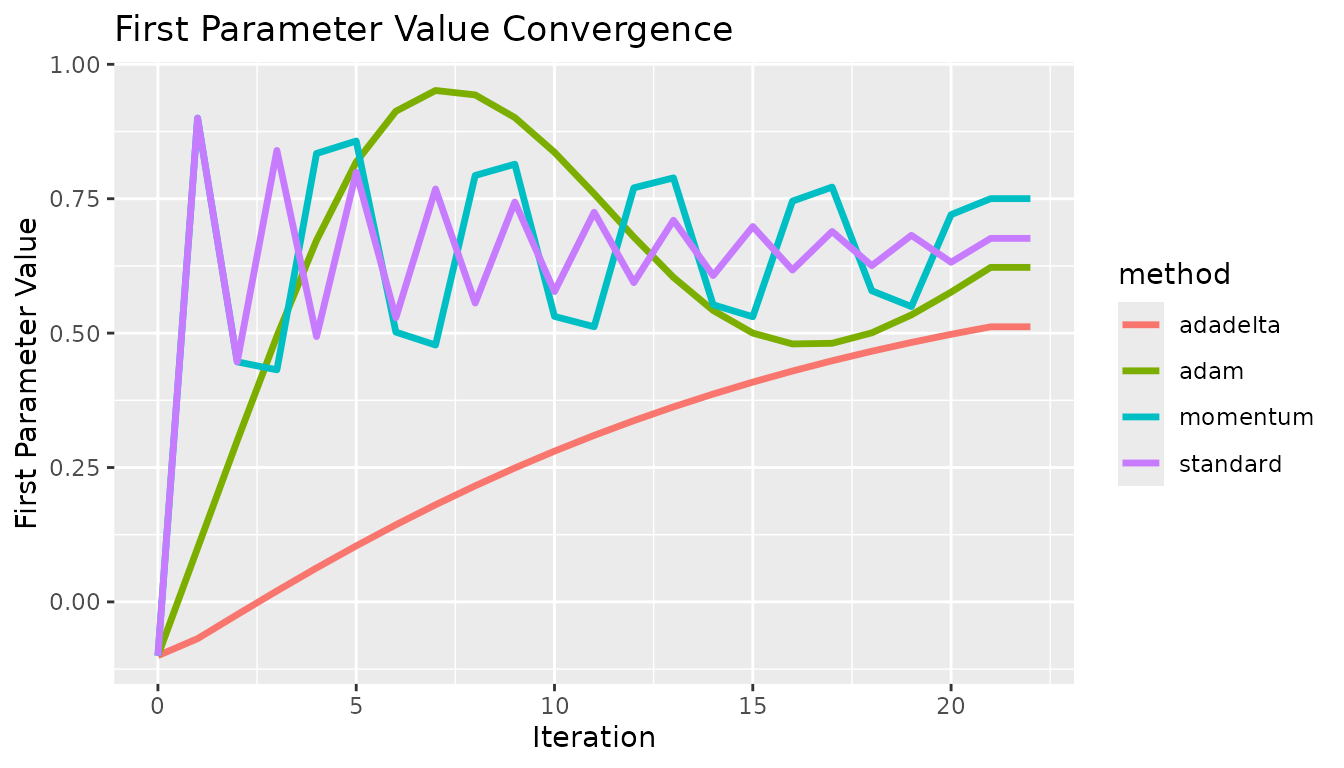

x <- c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)
y <- c(239.962, 234.592, 234.454, 234.362, 234.282, 234.226, 234.178, 234.144, 234.116, 234.094, 234.076, 234.062, 234.052, 234.044, 234.038, 234.032, 234.028, 234.026, 234.022, 234.02, 234.02, 234.018, 234.018, 239.962, 234.592, 234.454, 234.494, 234.362, 234.416, 234.284, 234.344, 234.226, 234.292, 234.174, 234.244, 234.142, 234.204, 234.112, 234.17, 234.092, 234.144, 234.072, 234.122, 234.06, 234.102, 234.102, 239.962, 239.438, 238.74, 238.104, 237.536, 237.036, 236.598, 236.22, 235.89, 235.608, 235.364, 235.156, 234.978, 234.826, 234.696, 234.586, 234.492, 234.414, 234.348, 234.292, 234.244, 234.206, 234.206, 239.962, 237.064, 235.166, 234.276, 234.118, 234.34, 234.642, 234.804, 234.766, 234.58, 234.334, 234.122, 234.018, 234.042, 234.142, 234.246, 234.298, 234.286, 234.23, 234.158, 234.09, 234.04, 234.04)
c <- c("standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "standard", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "momentum", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adadelta", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam", "adam")

df <- data.table("x" = x, "y" = y, "method" = c)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y, group = .data$method, color = .data$method)) +
  ggplot2::geom_line("linewidth" = 1.2) +
  ggplot2::labs(x = "Iteration", y = "Log-Likelihood Value") +
  ggplot2::ggtitle("Log-Likelihood Convergence")
g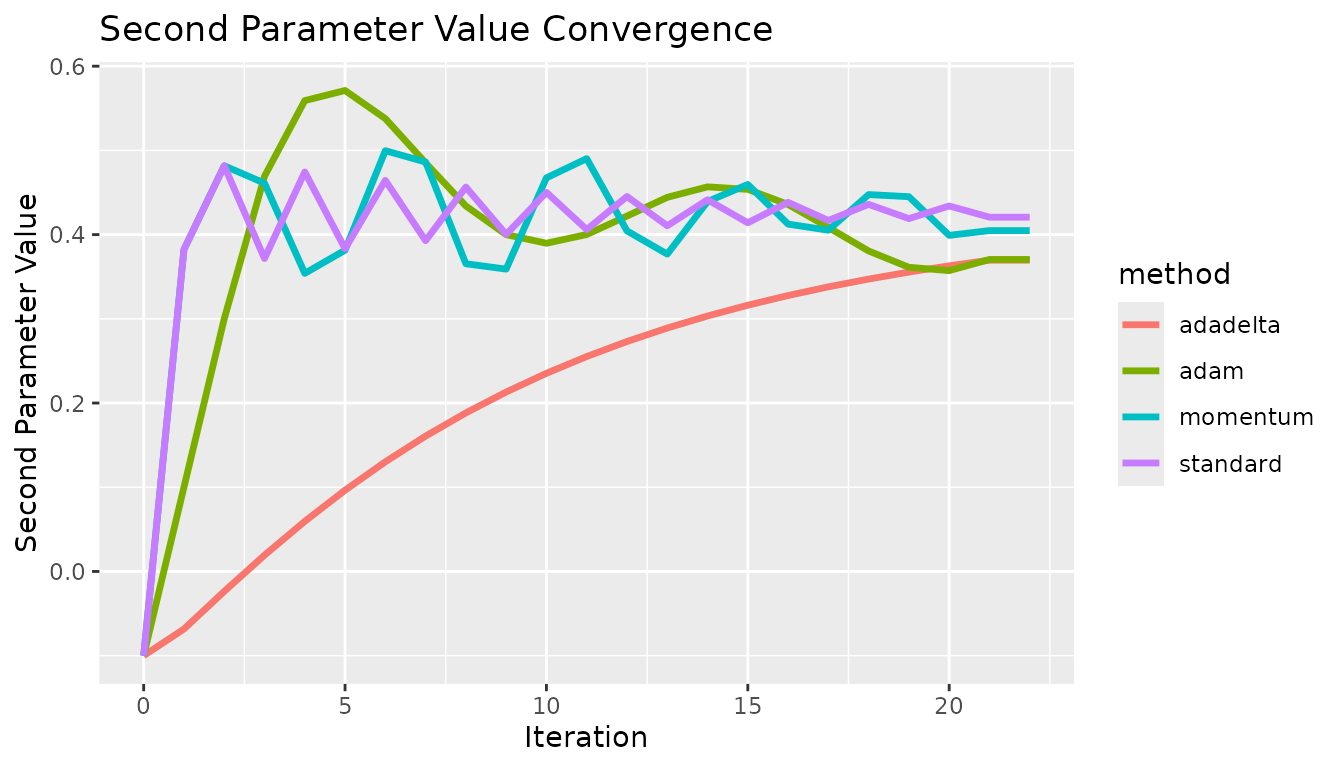

Hyper-parameter Tuning Examples

First a brief comparison of learning rates with the standard gradient descent method. For this analysis, the gradient was on the scale of (-2,2) so a learning rate on the scale of ~ 1/10 was appropriate. If the gradient were much larger then the learning rate would need to be correspondingly decreased. If the learning rate is too high, then the estimate will be unstable and oscillate. If the learning rate is too low then the estimate will not converge in a reasonable amount of time.

x <- c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)
y <- c(-0.1, -0.0758866, -0.0524678, -0.0297801, -0.00784991, 0.0133049, 0.0336744, 0.053255, 0.0720488, 0.0900628, 0.107308, 0.123797, 0.139549, 0.154581, 0.168914, 0.18257, 0.195571, 0.207941, 0.219702, 0.230879, 0.241495, 0.251573, 0.251573, -0.1, 0.141134, 0.305602, 0.376672, 0.406159, 0.418355, 0.423402, 0.425492, 0.426358, 0.426717, 0.426865, 0.426927, 0.426952, 0.426963, 0.426967, 0.426969, 0.42697, 0.42697, 0.42697, 0.42697, -0.1, 0.382267, 0.481728, 0.371577, 0.474396, 0.383262, 0.464408, 0.392812, 0.456452, 0.40023, 0.45019, 0.406007, 0.445259, 0.41052, 0.441374, 0.414052, 0.438314, 0.416821, 0.435902, 0.418993, 0.434002, 0.420699, 0.420699, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, -0.1, 0.9, 0.9)
c <- c("0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.01", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.1", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5")

df <- data.table("x" = x, "y" = y, "LearningRate" = c)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y, group = .data$LearningRate, color = .data$LearningRate)) +
  ggplot2::geom_line("linewidth" = 1.2) +
  ggplot2::labs(x = "Iteration", y = "Second Parameter") +
  ggplot2::ggtitle("Second Parameter Convergence")
g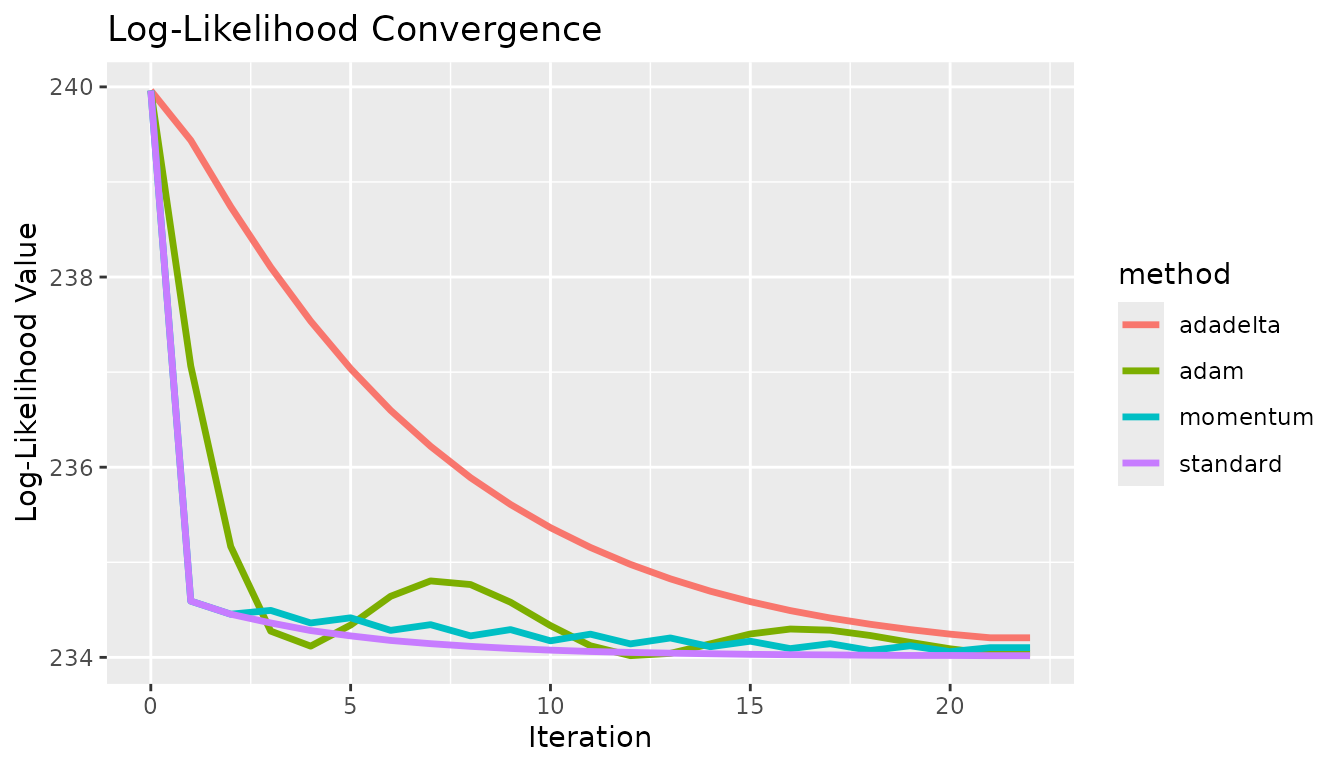

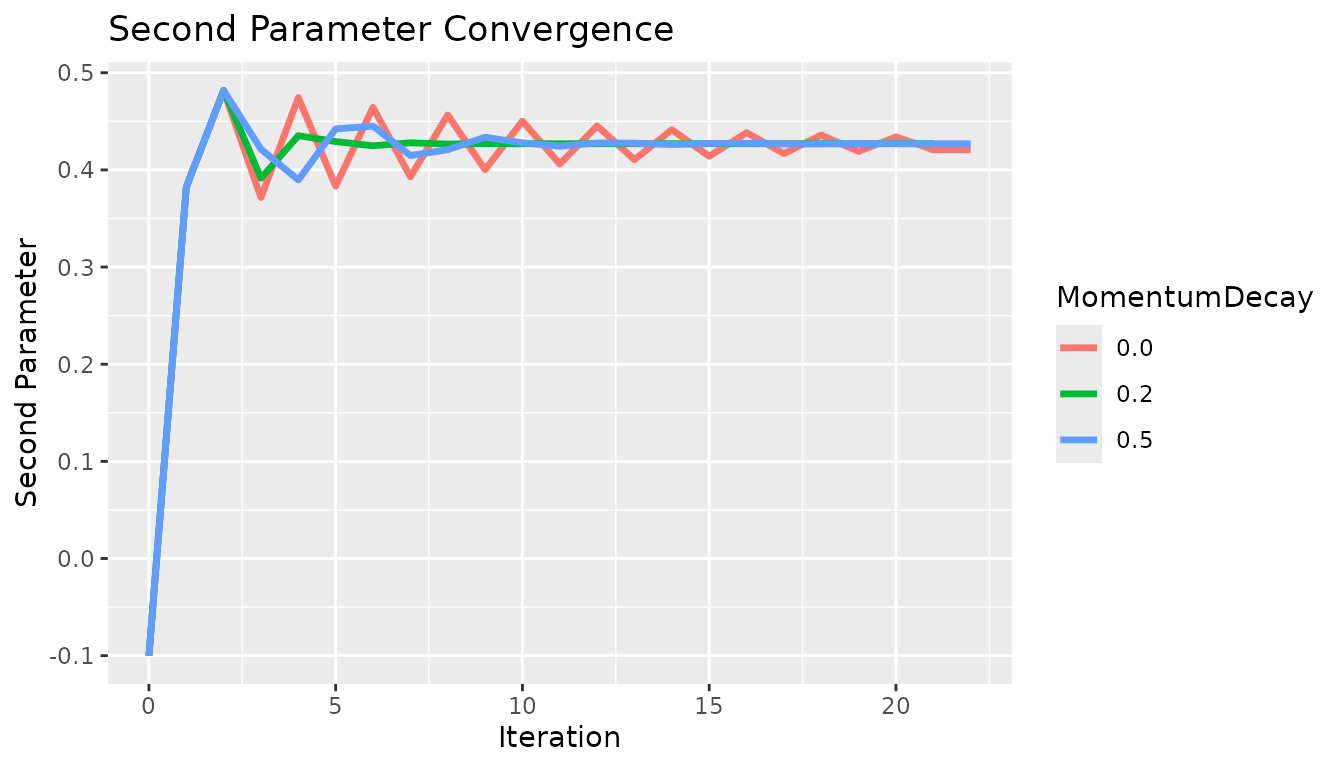
Next the momentum decay. The momentum decay term is helpful in particular when the standard method overshoots the solution. In this example the standard method at a learning rate of 0.1 has no issue overshooting the solution, so I tested the momentum method at a learning rate of 0.2 to induce oscillation. At a learning rate of 0.0 we have the standard gradient descent, and as we increase the momentum effect we see faster convergence.

x <- c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)
y <- c(-0.1, 0.382267, 0.481728, 0.371577, 0.474396, 0.383262, 0.464408, 0.392812, 0.456452, 0.40023, 0.45019, 0.406007, 0.445259, 0.41052, 0.441374, 0.414052, 0.438314, 0.416821, 0.435902, 0.418993, 0.434002, 0.420699, 0.420699, -0.1, 0.382267, 0.481728, 0.391469, 0.435244, 0.429155, 0.424804, 0.427892, 0.426568, 0.427082, 0.427015, 0.426915, 0.426992, 0.426967, 0.42697, 0.426971, 0.42697, 0.426971, 0.42697, 0.42697, 0.426971, 0.426971, -0.1, 0.382267, 0.481728, 0.421307, 0.389624, 0.442182, 0.445048, 0.414796, 0.420771, 0.433596, 0.427802, 0.424361, 0.427741, 0.42752, 0.426131, 0.427168, 0.427483, 0.426655, 0.426746, 0.427195, 0.427034, 0.426856, 0.426856)
c <- c("0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.0", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.2", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5", "0.5")

df <- data.table("x" = x, "y" = y, "MomentumDecay" = c)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y, group = .data$MomentumDecay, color = .data$MomentumDecay)) +
  ggplot2::geom_line("linewidth" = 1.2) +
  ggplot2::labs(x = "Iteration", y = "Second Parameter") +
  ggplot2::ggtitle("Second Parameter Convergence")
g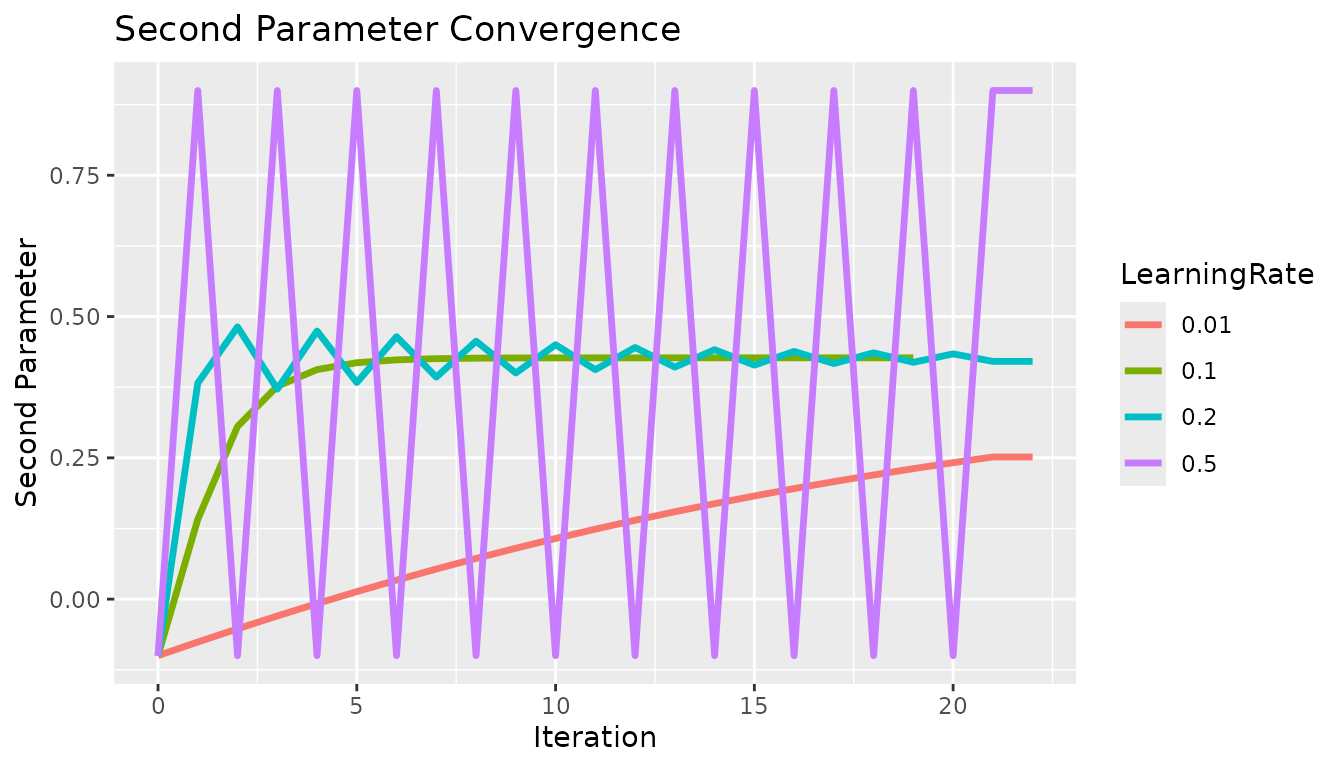

Finally we have the epsilon offset used in the adadelta method. In this example if the offset is too low the change in parameter value per iteration is near zero, then as it is increased the algorithm converges faster until the estimate oscillates.

x <- c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)
y <- c(-0.1, -0.0998946, -0.0997455, -0.0995686, -0.0993678, -0.0991457, -0.0989042, -0.0986448, -0.0983686, -0.0980766, -0.0977695, -0.0974482, -0.0971132, -0.096765, -0.0964041, -0.0960311, -0.0956462, -0.0952498, -0.0948422, -0.0944238, -0.0939948, -0.0935554, -0.0935554, -0.1, -0.0894592, -0.0745523, -0.0569106, -0.0369613, -0.0149815, 0.00881833, 0.0342662, 0.0612136, 0.0895258, 0.119075, 0.149732, 0.181361, 0.213808, 0.246885, 0.280336, 0.313768, 0.346445, 0.376444, 0.393247, 0.380437, 0.397974, 0.397974, -0.1, -0.0666699, -0.0195369, 0.0357806, 0.0976085, 0.164622, 0.235362, 0.307561, 0.375392, 0.39949, 0.393904, 0.42769, 0.416127, 0.448594, 0.412644, 0.445826, 0.410436, 0.445034, 0.409797, 0.444717, 0.409586, 0.444599, 0.444599, -0.1, 0.00530869, 0.154075, 0.317511, 0.438734, 0.311745, 0.479287, 0.359676, 0.509816, 0.380595, 0.519051, 0.390015, 0.516403, 0.39013, 0.51552, 0.389794, 0.484692, 0.374198, 0.483729, 0.372471, 0.483021, 0.372011, 0.372011)
c <- c("1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-8", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-4", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-3", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2", "1e-2")

df <- data.table("x" = x, "y" = y, "Epsilon" = c)

g <- ggplot2::ggplot(df, ggplot2::aes(x = .data$x, y = .data$y, group = .data$Epsilon, color = .data$Epsilon)) +
  ggplot2::geom_line("linewidth" = 1.2) +
  ggplot2::labs(x = "Iteration", y = "Second Parameter") +
  ggplot2::ggtitle("Second Parameter Convergence")
g